Методы рентгеновской и оптической дифракции

Учебные материалы по биологии / Использование дифракционных методов для анализа структуры, фракционного состава и равновесных взаимодействий биологических макромолекул / Методы рентгеновской и оптической дифракции

Страница 1

Рассеяние плоской волны веществом

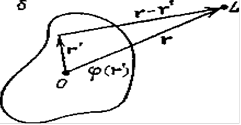
Пусть плоская монохроматическая волна A0exp(ik0r) падает на рассеивающий центр О, который под действием излучения становится источником сферической волны (рис. 1). Тогда в точке наблюдения L, результирующая волна имеет вид [14].

(2.1)

Здесь k0 и k - волновые векторы падающей и рассеянной волн, |k0| = |k|= 2π/λ, λ - длина волны, А0 и А0b/|r

| - амплитуды этих волн, r

- вектор, соединяющий точку L с рассеивающим центром в точке О. Амплитуда рассеянной сферической волны равна произведению амплитуды падающей волны и коэффициента b/|r|, где значение b определяется видом падающего излучения и природой рассеивающего центра, находящегося в точке О. Чем сильнее взаимодействие падающей волны с центром О, тем больше коэффициент b. Он имеет размерность длины и носит название длины рассеяния, или амплитуды рассеяния точечного центра. Рассеяние плоской монохроматической волны на реальных объектах, состоящих из совокупности ядер и электронов, можно рассматривать как точечные рассеивающие центры.

Рис. 1. Рассеяние плоской волны точечным центром (а) и ограниченной областью, задаваемой потенциалом φ(r') (б)

Рассеивающую способность произвольного скопления ядер, электронов при облучении их рентгеновскими лучами или светом можно характеризовать рассеивающей плотностью φ(r) - скалярным полем, заданным в ограниченной области пространства. Для рентгеновского рассеяния φ(r) - плотность распределения заряда, в случае света - это оптическая плотность вещества, зависящая от показателя преломления. Взаимодействие волны (рентгеновского излучения или света) с веществом можно представить себе таким образом, что волна электромагнитного излучения взаимодействует со всеми ядрами, электронами и валентными оболочками, которые становятся источниками сферических волн. Суперпозиция этих волн представляет собой первое приближение к реальному рассеянию. Можно показать, что функция

(2.2)

является амплитудой упругого рассеяния на скалярном поле φ(r). Это - так называемое первое борновское приближение, иными словами - приближение однократного рассеяния.

Выражение (2.2) представляет собой интеграл Фурье, т.е. разложение функции f(h) по базисной системе ортогональных функций - экспоненциальных функций exp(ihr). Решение обратной задачи - нахождения φ(r) при известной функции f(h) - дается обратным преобразованием [14]

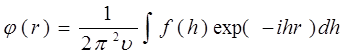(2.3)

Таким образом, преобразования Фурье лежат в основе расчетов амплитуд рассеяния по заданной системе рассеивающих центров и плотности поля рассеяния по заданной амплитуде рассеяния, если, разумеется, выполнены условия первого борновского приближения. При определении атомной и молекулярной структуры вещества стараются всегда так поставить эксперимент, чтобы это приближение (и тем самым взаимные интегральные фурье-преобразования (2.2) и (2.3) для амплитуды и плотности рассеяния) выполнялось. Экспериментально определяется не сама амплитуда рассеяния, а интенсивность I(h), пропорциональная квадрату амплитуды рассеяния:

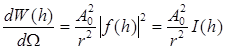(2.4)

Ω - телесный угол). Функция I(s) называется интенсивностью рассеяния (название, принятое в рентгеноструктурном анализе и в светорассеянии). Видно, что размерность этой функции - квадрат длины. Важной характеристикой объекта является полная интенсивность (или полное сечение) рассеяния, которая дается интегрированием (2.4) по всем углам:

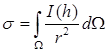(2.5)

Главной задачей структурного анализа вещества является восстановление распределения рассеивающей плотности φ(r) по измеренной функции I(h) [14, 15].

Формула Гинье. Угловое разрешение

С точностью до h4 имеем разложение интенсивности I(h) в близи точки h = 0 [14, 15]:

(2.6)

Выражение в скобках в правой части (2.6) можно рассматривать как первые два члена разложения в ряд Маклорена функции ехр(-h2R2g/3). Поэтому с точностью до членов, пропорциональных h4, для начальной части кривой рассеяния можно записать